On va commencer simple et expliquer l’utilité d’un pont diviseur de tension.

Explications

Partons du principe que nous avons une alimentation de 9v.

• d’un bout à l’autre du circuit, la tension est de 9v

Si maintenant on souhaite alimenter un composant, cela ne pourrait pas fonctionner car la tension est trop élevé. (Et il faut bien évidemment que le composant est besoin d’une toute petite puissance pour fonctionner.)

Il faut donc :

• soit baisser la tension : mais là, le souci c’est que tout le circuit aura la tension baissé et c’est pas forcement ce que l’on souhaite
• soit diviser la tension via un pont diviseur : en utilisant 2 résistances. La division de la tension permettra d’avoir en sortie de la résistance 1 la tension souhaitée

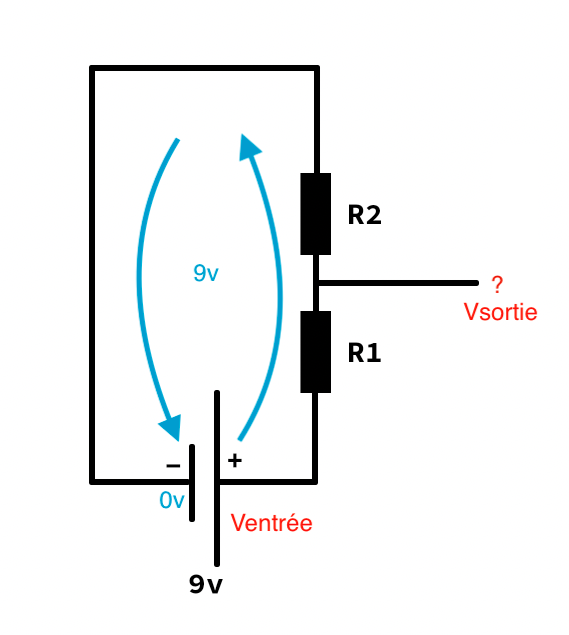
Comme on l’a dit juste avant, on part sur du 9v. Et on va ajouter 2 résistances :

• R1 : 10 000 Ω
• R2 : 4 500 Ω

Et maintenant il faut trouver la valeur de la tension entre nos 2 résistances : heureusement, il y a une formule pour cela :

Vsortie = Ventrée * R2 / ( R1 + R2 )

Partant de là, on va pouvoir remplacer par les valeurs et ainsi avoir notre résultat :

• Vs = Ve * R2 / ( R1 + R2 )
• Vs = 9 * 4 500 / ( 10 000 + 4 500)
• VS = 2,793103448
• on peut arrondir à 2,8v

Cas avec l’arduino

Imaginons que nous avons une carte UNO et que pour une raison (un composant par exemple) il nous faut une tension de 1v pour éviter de détériorer ce composant.

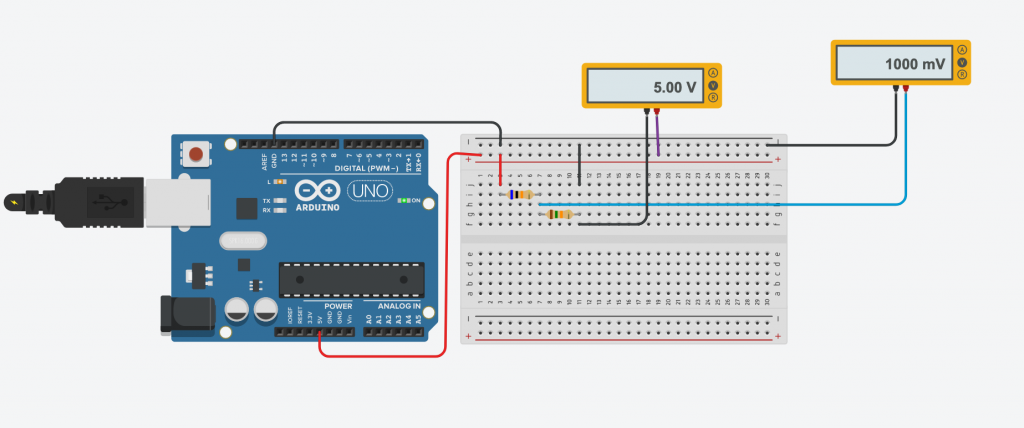
Repartons avec notre formule : Vs = Ve * R2 / ( R1 + R2 )

• Vs = 5 * 5 000 / ( 20 000 + 5 000 )
• Vs = 1v

Vous allez me dire, mmm comment j’ai su les résistantes à utiliser ? On peut tester jusqu’à trouver mais bon c’est bof bof. L’autre option c’est modifier la fonction afin de chercher une résistance :

R1 = R2 * ( Ventrée / Vsortie ) – R2

On reprend notre exemple : l’arduino nous donne 5v et on a besoin à un moment d’1v pour un composant. L’idée maintenant c’est partir sur une résistance au hasard et la formule nous donnera la 2e résistance.

Partons sur une résistance R2 de 68 000 Ω

• R1 = 68 000 * ( 5v / 1v ) – 68 000
• R1 = 68 000 * 5 – 68 000
• R1 = 340 000 – 68 000
• R1 = 272 000 Ω

Et on a notre solution. Si l’on souhaite partir de 5v et avoir 1v en utilisant une résistance de 68 000 Ω, il nous faudra une 2e résistance de 272 000 Ω pour que le pont diviseur de tension fonctionne.

Exemple

Et si maintenant, on part de 9v et on souhaite 3,3v vous savez comment faire :

On commence par choisir une résistance au hasard : 330 Ω

• R1 = 330 * ( 9v / 3,3v ) – 330
• R1 = 330 * 2,727272727 – 330
• R1 = 899,99999991 – 330
• R1 = 569,99999991 Ω

On peut arrondir à 570 Ω

Le rôle des résistances dans le pont

Partons de nos 2 exemples :

• Arduino : 5v avec R1 = 272KΩ et R2 = 68KΩ nous donne 1v
• Une pile 9v : avec R1 570Ω et R2 330Ω nous donne 3,3v

Dans la première situation on a des résistances beaucoup plus importantes que dans le 2e cas.

Est-ce que cela fait une différence ? et la réponse OUI !

Le courant (mah) va varier en fonction de la capacité de la résistance. Plus elle sera élevé et moins de courant passera. Par contre, la tension(v), elle ne bougera pas ou très peu à partir du moment qu’il y a un ordre de grandeur respecté.

Un exemple pour illustrer cela dans la partie suivante.

A savoir sur le pont

Pour bien l’utiliser, il faut connaitre la loi d’ohm :

• U = I x R

Que l’on peut décliner pour chercher les autres choses :

• I = U / R
• R = U / I

Et pour la légende :

• I c’est l’intensité du courant qui circule (des Ampères)
• U c’est la tension aux bornes de la résistance (des volts)
• R c’est la valeur de la résistance (des Ohms)

Et grâce à cela on va pouvoir calculer l’intensité du courant qui circule dans un pont diviseur. On repart sur l’exemple de la pile 9v : avec R1 570Ω et R2 330Ω nous donne 3,3v

• I = 9v / ( 570 + 330 )
• I = 0,01 A soit 10 mA

Et si on augmente les résistances :

• I = 9v / ( 34545 + 20000 )
• I = 0,000165001375 A soit 165 uA

Ici on voit la différence du courant en fonction de la capacité des résistances.

Cas concret loi d’ohm + pont diviseur

• batterie de 5v
• un esp8266-01 qui fonctionne en 3,3v (si vous voulez en savoir plus c’est ici)

Donc ici l’énigme c’est comment utiliser la batterie de 5v pour faire fonctionner correctement l’ESP sans tout faire sauter ? 😀

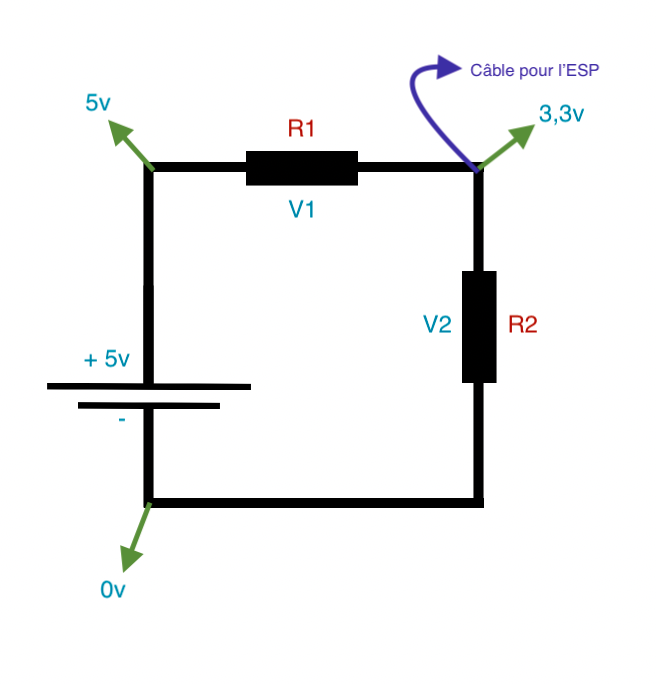
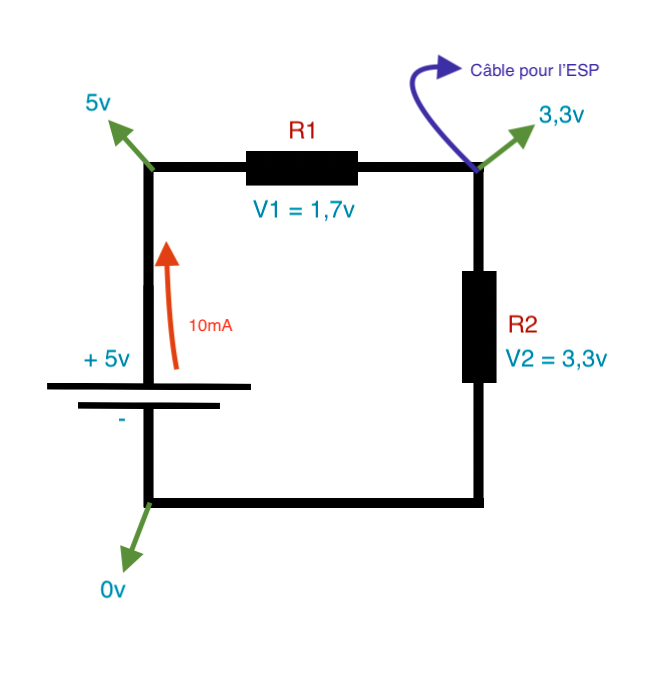
Voici le schéma :

Voici ce qu’on connait :

• 5v de la batterie
• le 3,3 v que l’on souhaite obtenir

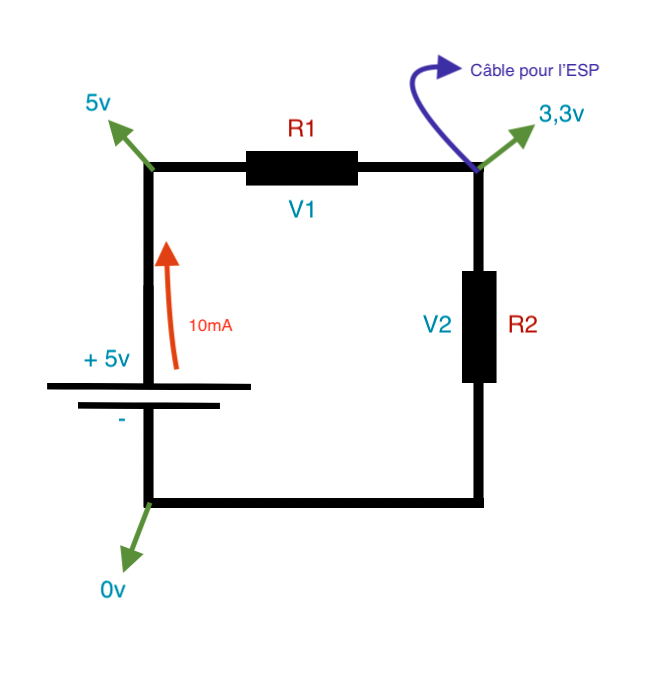
On va continuer en imaginant que l’on souhaite 10mA dans le circuit.

Partant de là, on sait que les 2 résistances en série c’est comme si on avait R1 + R2 = R3. On partira de R3 pour les calcules.

La loi d’ohm : U = R * I

On peut remplacer par ce que l’on connait : 5v = R3 * 0,01 A

On recherche R3 donc R3 = 5v / 0,01 A = 500 Ω

Ici on sait que R1 + R2 = 500 Ω afin d’avoir un courant de 10mA dans notre circuit alimenté par du 5v.

Il reste à trouver comment calculer R1 et R2.

En réfléchissant un peu, on connait une autre chose : V2 et V1. On souhaite du 3,3v entre nos 2 résistances donc la tension aux bornes de la résistance R2 doit être normalement à 3,3v.

Par conséquent

• V2 = 3,3v
• V1 = 5v – 3 ,3v = 1,7v

On peut reprendre notre calcule avec la formule du pont diviseur de tension : Vsortie = Ventrée * R2 / ( R1 + R2 )

Et on remplace : 3,3v = 5v * R2 / R3 On n’oublie pas ce qu’on a fait juste avant car on sait que R3 = R1 + R2 = 500 Ω

Donc :

• 3,3v = 5v * R2 / 500 Ω
• R2 = 500 Ω / 5v * 3,3
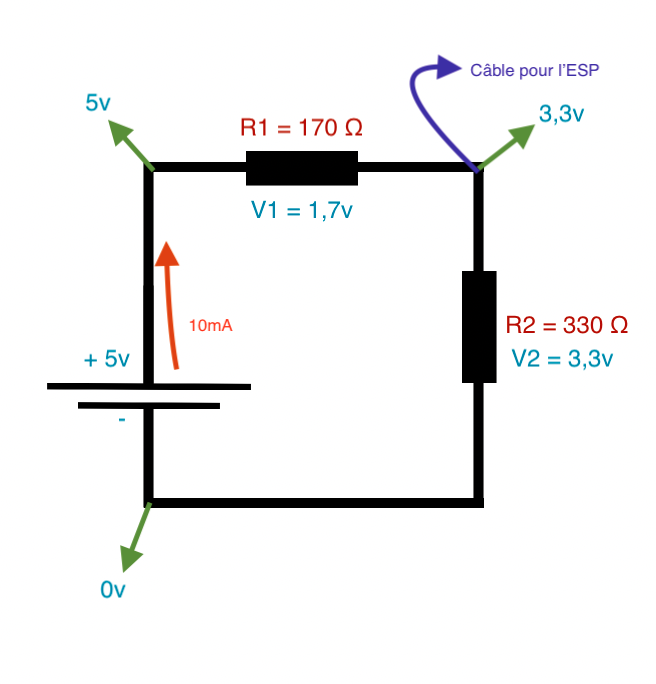
• R2 = 330 Ω

Et maintenant même plus besoin d’une autre formule car on a tout ce qu’il faut pour trouver R1 :

• R3 = R1 + R2
• 500 = R1 + 330
• R1 = 500 – 330
• R1 = 170 Ω

TADAAA

Calculateur de diviseur de tension

• Je cherche la tension de sortie
• Je cherche la 2e résistance

Partage :

Facebook

Twitter